Problem statement

The numeric value of a lowercase character is defined as its position (1-indexed) in the alphabet, so the numeric value of a is 1, the numeric value of b is 2, the numeric value of c is 3, and so on.

The numeric value of a string consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string "abe" is equal to 1 + 2 + 5 = 8.

You are given two integers n and k. Return the lexicographically smallest string with length equal to n and numeric value equal to k.

Note that a string x is lexicographically smaller than string y if x comes before y in dictionary order, that is, either x is a prefix of y, or if i is the first position such that x[i] != y[i], then x[i] comes before y[i] in alphabetic order.

Example 1

Input: n = 3, k = 27
Output: "aay"
Explanation: The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.

Example 2

Input: n = 5, k = 73
Output: "aaszz"

Constraints

• 1 <= n <= 10^5.
• n <= k <= 26 * n.

Solution 1: Adding each character as small as possible

Construct the result from scratch, from left to right.

For each position, add the smallest possible character.

Let us call the resulting string s. To compute the smallest possible character for s[i], you can assume the remaining letters after s[i] are all z.

Example

For n = 3, k = 27.

• Assume s = "?zz". Then k - "zz" = 27 - 52 = -25 <= 'a'. So s[0] can be 'a'.
• Assume s = "a?z". Then k - "az" = 27 - 27 = 0 <= 'a'. So s[1] can be 'a'.
• Now s = "aa?" and k - "aa" = 27 - 2 = 25 = 'y'. So s[2] = 'y'.
• s = "aay".

Code

#include <iostream>
using namespace std;
string getSmallestString(int n, int k) {
    string s;
    while (n > 0) {
        int i = k - 26*(n - 1); // assume remain letters are all 'z'
        char c = i <= 1 ? 'a' : 'a' + i - 1;
        s += c; 
        k -= c - 'a' + 1;
        n--;
    }
    return s;
}
int main() {
    cout << getSmallestString(3, 27) << endl;
    cout << getSmallestString(5, 73) << endl;
}

Output:
aay
aaszz

Complexity

• Runtime: O(n).
• Extra space: O(1).

Solution 2: Adjust the result from "aa...a"

You can do the other way around by starting from s = "aa...a" and adjusting each letter 'a' from right to left to be the biggest possible.

Example 2

For n = 5 and k = 73:

• Starting with s = "aaaaa".
• k becomes 73 - "aaaaa" = 68, which is big enough to make the last 'a' becomes 'z': s = "aaaaz".
• k becomes 73 - "aaaaz" = 43, which is big enough to make the next 'a' becomes 'z': s = "aaazz".
• k becomes 73 - "aaazz" = 18, which make the next 'a' becomes 's': s = "aaszz".
• s = "aaszz".

#include <iostream>
#include <string>
using namespace std;
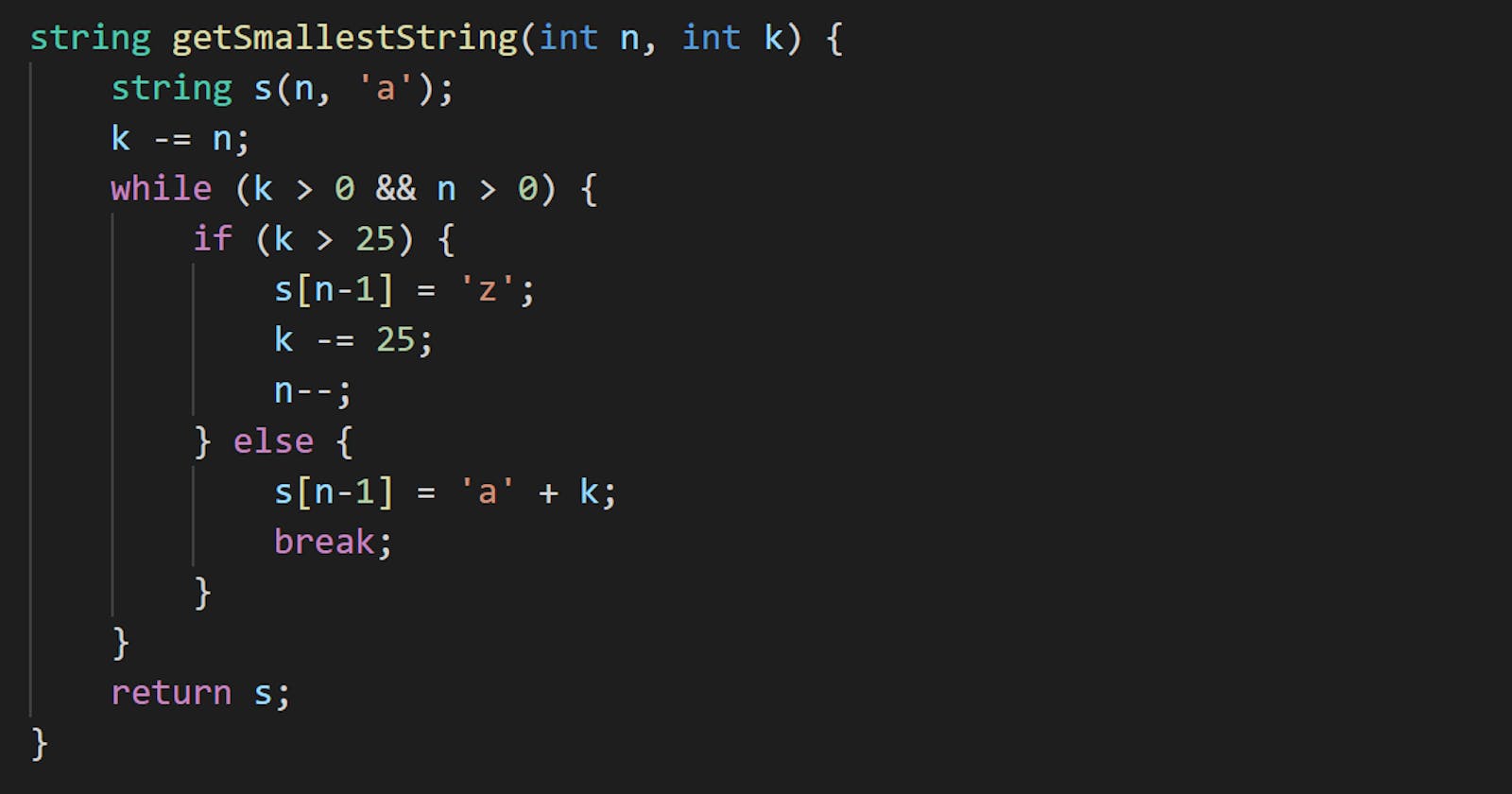
string getSmallestString(int n, int k) {
    string s(n, 'a');
    k -= n;
    while (k > 0 && n > 0) {
        if (k > 25) {
            s[n - 1] = 'z';
            k -= 25;
            n--;
        } else {
            s[n - 1] = 'a' + k;
            break;
        }
    }
    return s;
}
int main() {
    cout << getSmallestString(3, 27) << endl;
    cout << getSmallestString(5, 73) << endl;
}

Output:
aay
aaszz

Complexity

• Runtime: O(n). But it is faster than Solution 1 since there are fewer operations, especially there is no multiplication.
• Extra space: O(1).