Problem statement
You are given an n x n 2D matrix representing an image. Rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1
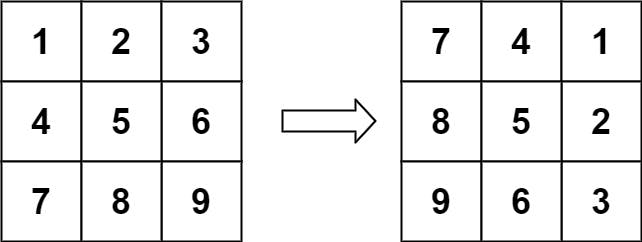
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]
Example 2

Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Constraints
n == matrix.length == matrix[i].length.1 <= n <= 20.-1000 <= matrix[i][j] <= 1000.
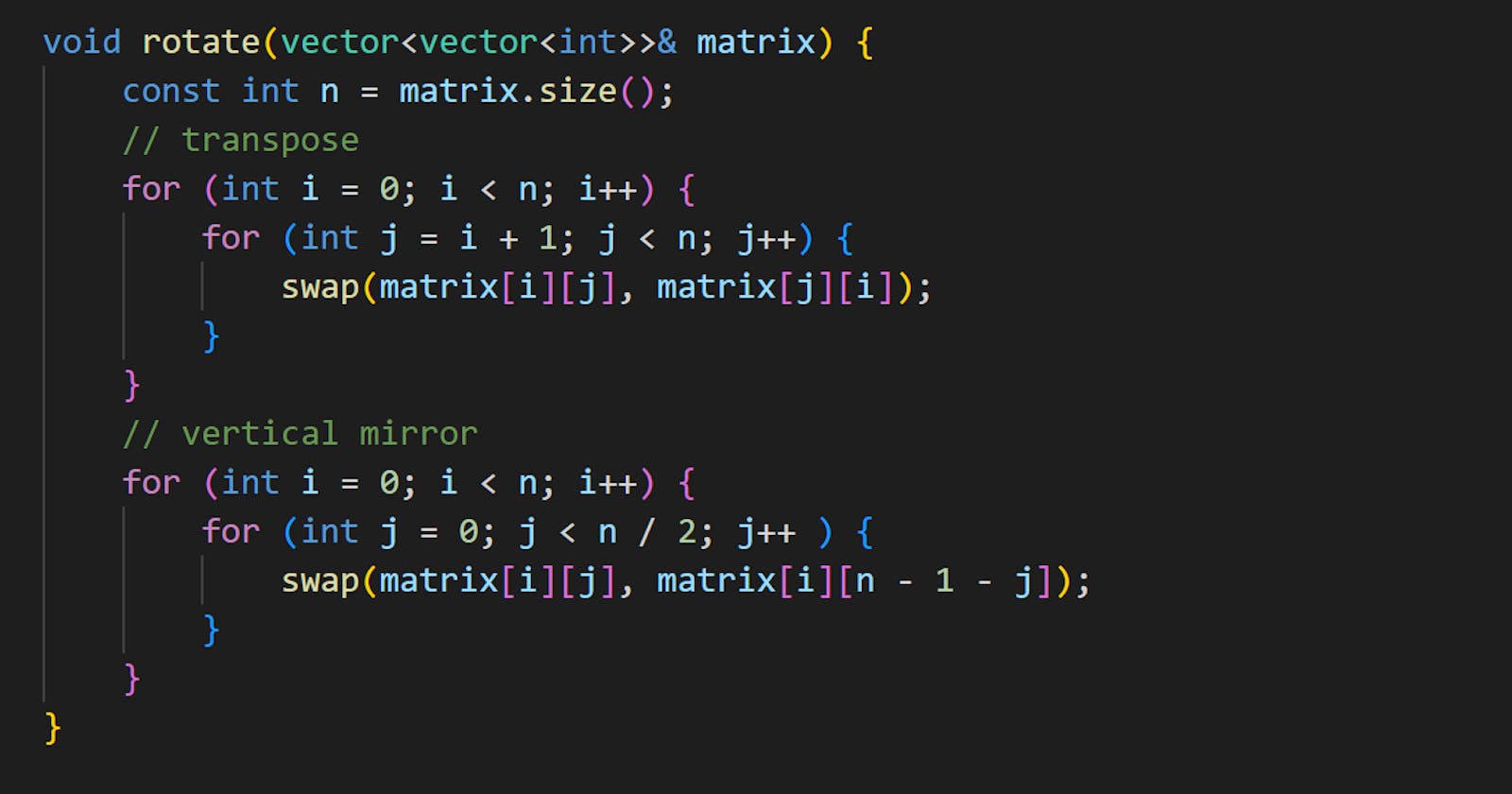
Solution: The math behind
For any square matrix, the rotation 90 degrees clockwise can be performed by two steps:
Transpose the matrix.
Mirror the matrix vertically.
Code
#include <iostream>
#include <vector>
using namespace std;
void rotate(vector<vector<int>>& matrix) {
const int n = matrix.size();
// transpose
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
swap(matrix[i][j], matrix[j][i]);
}
}
// vertical mirror
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++ ) {
swap(matrix[i][j], matrix[i][n - 1 - j]);
}
}
}
void printMatrix(vector<vector<int>>& matrix) {
cout << "[";
for (auto& row: matrix) {
cout << "[";
for (auto& a: row) {
cout << a << ",";
}
cout << "],";
}
cout << "]\n";
}
int main() {
vector<vector<int>> matrix{{1,2,3},{4,5,6},{7,8,9}};
rotate(matrix);
printMatrix(matrix);
matrix = {{5,1,9,11},{2,4,8,10},{13,3,6,7},{15,14,12,16}};
rotate(matrix);
printMatrix(matrix);
}
Output:
[[7,4,1,],[8,5,2,],[9,6,3,],]
[[15,13,2,5,],[14,3,4,1,],[12,6,8,9,],[16,7,10,11,],]
Complexity
Runtime:
O(n^2), wheren = matrix.length.Extra space:
O(1).