Problem statement

Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), ans[i] is the number of 1's in the binary representation of i.

Example 1

Input: n = 2
Output: [0,1,1]
Explanation:
0 --> 0
1 --> 1
2 --> 10

Example 2

Input: n = 5
Output: [0,1,1,2,1,2]
Explanation:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

Constraints

• 0 <= n <= 10^5.

Solution 1: Count the binary representation using std::bitset

Code

#include <vector>
#include <iostream>
#include <bitset>
using namespace std;
vector<int> countBits(int n) {
    vector<int> ans;
    for (int i = 0; i <= n; i++) {
        bitset<17> b(i); // 17 bits to make sure it can exceed 10^5
        ans.push_back(b.count());
    }
    return ans;
}
void print(vector<int>& ans) {
    cout << "[";
    for (int a : ans) { 
        cout << a << ",";
    }
    cout << "]\n";
}
int main() {
    auto ans = countBits(2);
    print(ans);
    ans = countBits(5);
    print(ans);
}

Output:
[0,1,1,]
[0,1,1,2,1,2,]

Complexity

• Runtime: O(nlogn).
• Extra space: O(1).

Solution 2: Finding the pattern

1. If you append a bit 0 to the binary representation of an integer i, you perform the operator i -> 2*i but the number of bits 1 is unchanged. In other words, ans[2*i] = ans[i].
2. If you append a bit 1 to the binary representation of i, you perform the operator i -> 2*i + 1 and the number of bits 1 is incremented one. In other words, ans[2*i + 1] = ans[i] + 1.

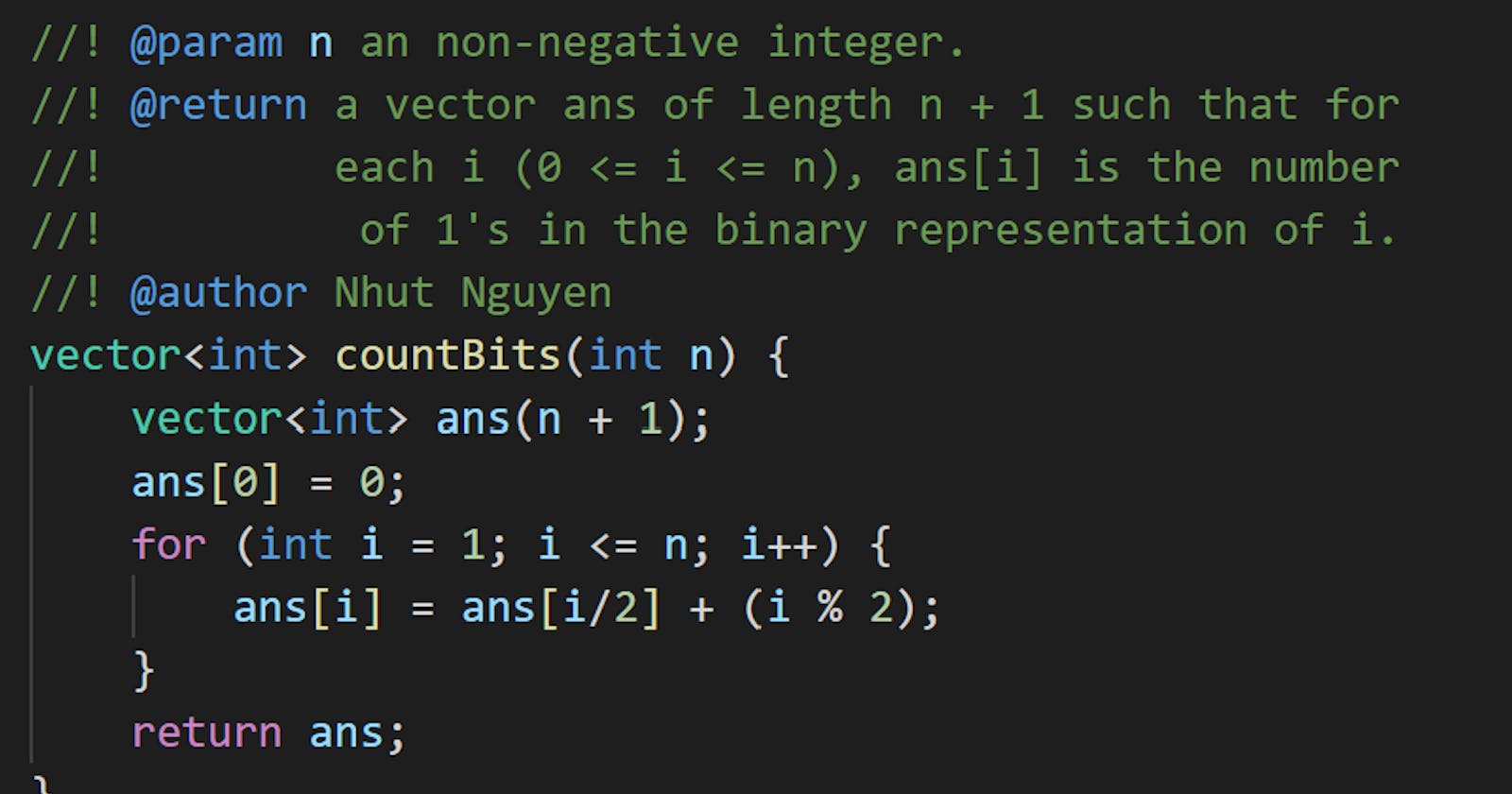
Code

#include <vector>
#include <iostream>
using namespace std;
vector<int> countBits(int n) {
    vector<int> ans(n + 1);
    ans[0] = 0;
    for (int i = 1; i <= n; i++) {
        ans[i] = ans[i/2] + (i % 2);
    }
    return ans;
}
void print(vector<int>& ans) {
    cout << "[";
    for (int a : ans) { 
        cout << a << ",";
    }
    cout << "]\n";
}
int main() {
    auto ans = countBits(2);
    print(ans);
    ans = countBits(5);
    print(ans);
}

Output:
[0,1,1,]
[0,1,1,2,1,2,]

Complexity

• Runtime: O(n).
• Extra space: O(1).