Problem statement

Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.

You must write an algorithm with O(log n) runtime complexity.

Example 1

Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

Example 2

Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1

Constraints

• 1 <= nums.length <= 10^4.
• -10^4 < nums[i], target < 10^4.
• All the integers in nums are unique.
• nums is sorted in ascending order.

Solution: Divide and Conquer

Since nums is sorted in ascending order you can divide it into subparts to find the target. You can use the middle elements of nums to divide the subparts. target might equal to that element, on the left subpart or in the right subpart.

Code

#include <vector>
#include <iostream>
using namespace std;
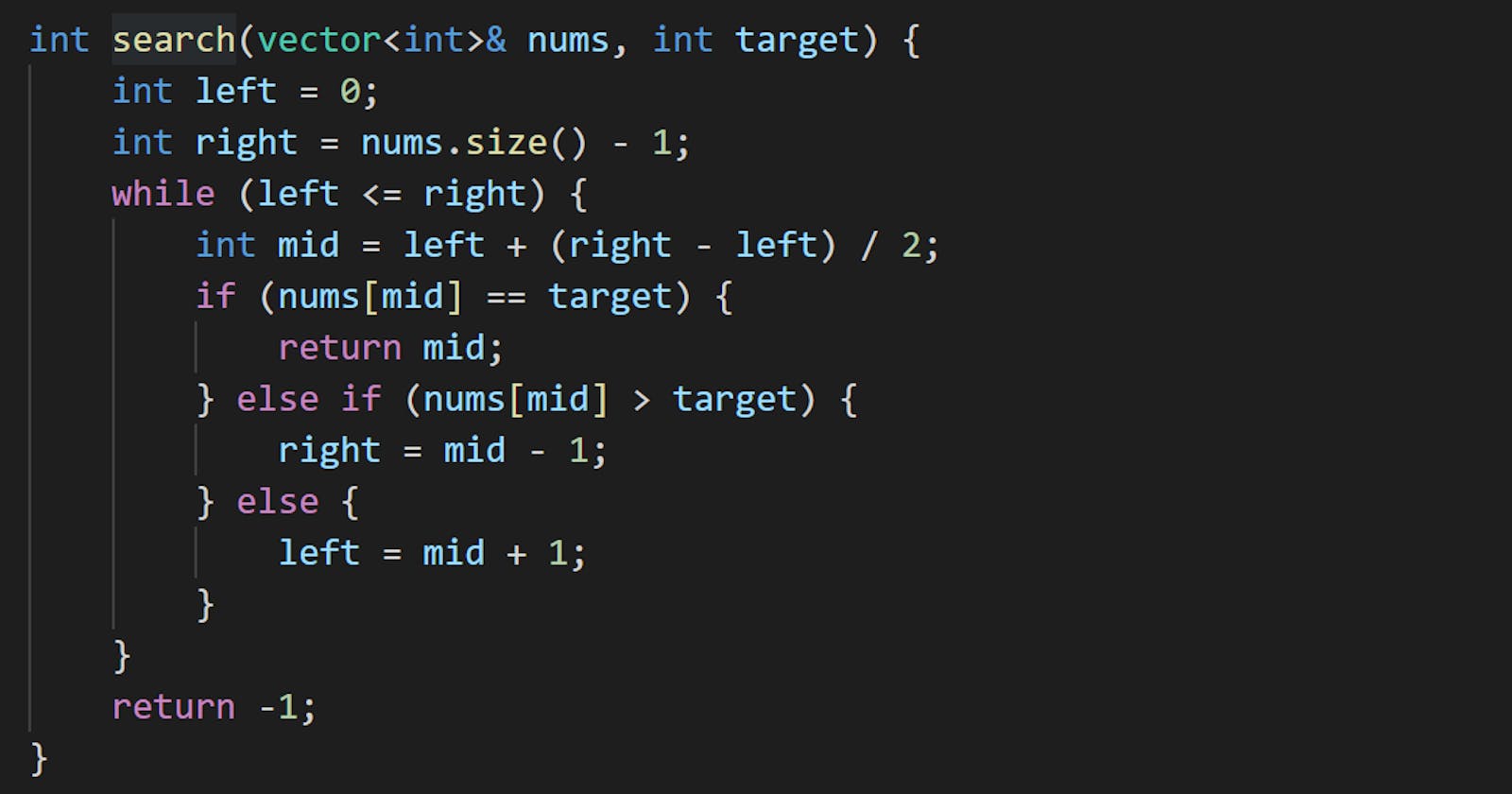
int search(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return -1;
}
int main() {
    vector<int> nums{-1,0,3,5,9,12};
    cout << search(nums, 9) << endl;
    cout << search(nums, 2) << endl;
}

Output:
4
-1

Complexity

• Runtime: O(logN) where N = nums.length.
• Extra space: O(1).

Implementation notes

• mid is actually (right + left) / 2. But (right + left) might be too big to be overflow before the division. To avoid that overflow you can rewrite the expression to mid = left + (right - left) / 2.