Problem statement

You are given an array people where people[i] is the weight of the i-th person, and an infinite number of boats where each boat can carry a maximum weight of limit. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most limit.

Return the minimum number of boats to carry every given person.

Example 1

Input: people = [1,2], limit = 3
Output: 1
Explanation: 1 boat (1, 2)

Example 2

Input: people = [3,2,2,1], limit = 3
Output: 3
Explanation: 3 boats (1, 2), (2) and (3)

Example 3

Input: people = [3,5,3,4], limit = 5
Output: 4
Explanation: 4 boats (3), (3), (4), (5)

Constraints

• 1 <= people.length <= 5 * 10^4.
• 1 <= people[i] <= limit <= 3 * 10^4.

Solution: Greedy

For each boat pick the heaviest person first. The remaining weight on that boat might be not enough for anyone else. Otherwise, let the lightest one go as well.

Example 2

For people = [3,2,2,1] and limit = 3:

• The heaviest one is 3. He reaches the limit. This boat can carry only him.
• The next heavy one is 2. This boat may carry one more with at most 1 in weight. The lightest one ( weight 1) satisfies that. They are on this same boat.
• The last boat carries the last person with weight 2.

Code

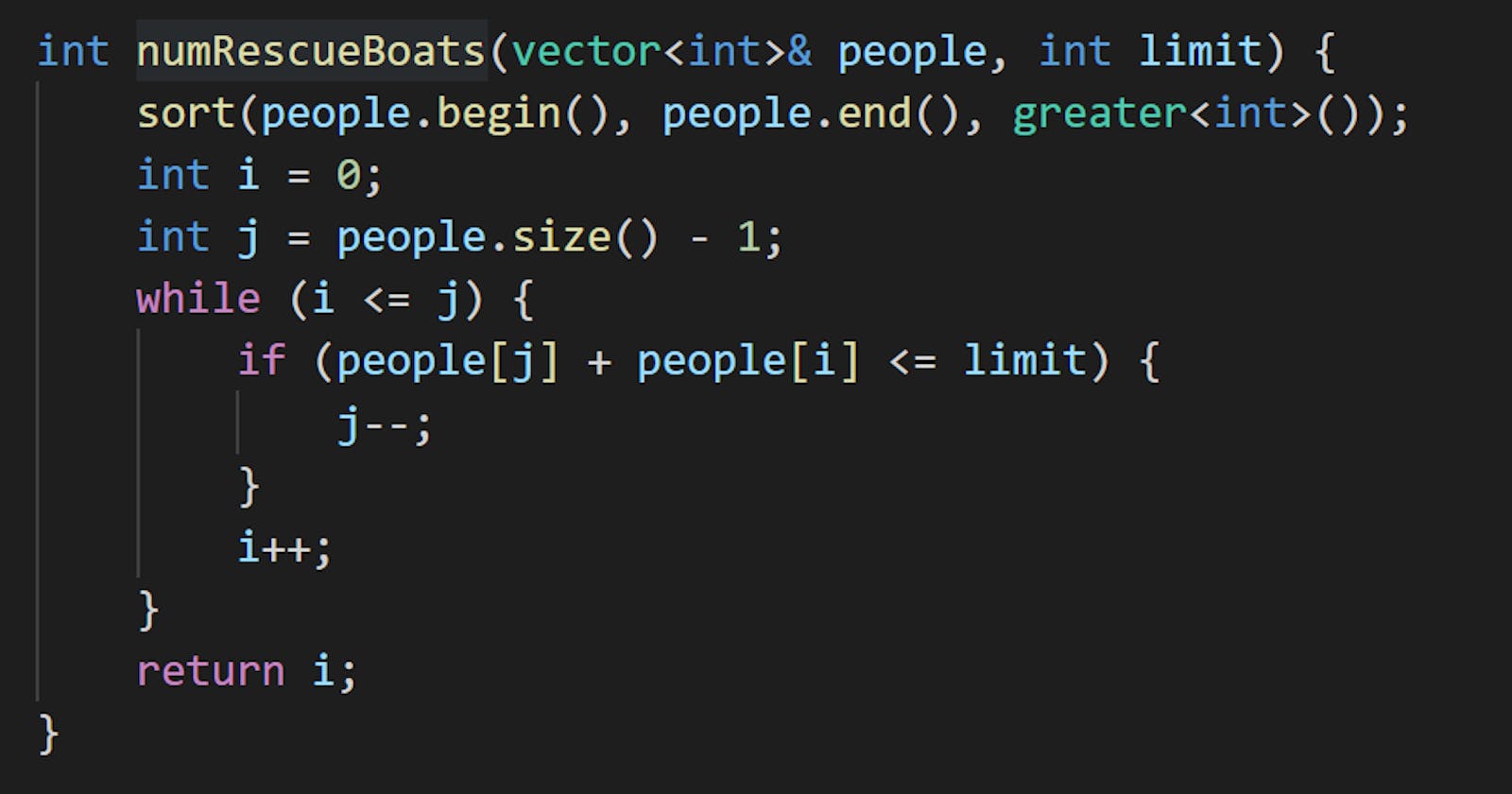
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int numRescueBoats(vector<int>& people, int limit) {
    sort(people.begin(), people.end(), greater<int>());
    int i = 0;
    int j = people.size() - 1;
    while (i <= j) {
        if (people[i] + people[j] <= limit) {
            j--;
        }
        i++;
    }
    return i;
}
int main() {
    vector<int> people{1,2};
    cout << numRescueBoats(people, 3) << endl;
    people = {1,2,3,2};
    cout << numRescueBoats(people, 3) << endl;
    people = {3,5,3,4};
    cout << numRescueBoats(people, 5) << endl;
}

Output:
1
3
4

Complexity

• Runtime: O(NlogN), where N = people.length.
• Extra space: O(1).