Problem statement
You are given an m x n integer grid accounts where accounts[i][j] is the amount of money the i-th customer has in the j-th bank. Return the wealth that the richest customer has.
A customer's wealth is the amount of money they have in all their bank accounts. The richest customer is the customer that has the maximum wealth.
Example 1
Input: accounts = [[1,2,3],[3,2,1]]
Output: 6
Explanation:
1st customer has wealth = 1 + 2 + 3 = 6
2nd customer has wealth = 3 + 2 + 1 = 6
Both customers are considered the richest with a wealth of 6 each, so return 6.
Example 2
Input: accounts = [[1,5],[7,3],[3,5]]
Output: 10
Explanation:
1st customer has wealth = 6
2nd customer has wealth = 10
3rd customer has wealth = 8
The 2nd customer is the richest with a wealth of 10.
Example 3
Input: accounts = [[2,8,7],[7,1,3],[1,9,5]]
Output: 17
Constraints
m == accounts.length.n == accounts[i].length.1 <= m, n <= 50.1 <= accounts[i][j] <= 100.
Solution: Bruteforce
Compute the wealth for each account to determine who is the richest.
Code
#include <vector>
#include <iostream>
using namespace std;
int maximumWealth(vector<vector<int>>& accounts) {
int maxWealth = 0;
for (int i = 0; i < accounts.size(); i++) {
int w = 0;
for (auto& money : accounts[i]) {
w += money;
}
maxWealth = max(maxWealth, w);
}
return maxWealth;
}
int main() {
vector<vector<int>> accounts{{1,2,3},{3,2,1}};
cout << maximumWealth(accounts) << endl;
accounts = {{1,5},{7,3},{3,5}};
cout << maximumWealth(accounts) << endl;
accounts = {{2,8,7},{7,1,3},{1,9,5}};
cout << maximumWealth(accounts) << endl;
}
Output:
6
10
17
Complexity
- Runtime
O(m*n), wherem = accounts.length,n == accounts[i].length. - Extra space:
O(1).
Modern C++ with std::accumulate()
Computing the sum of a vector v is a very common task. There are many ways to achieve it. One way is using function std::accumulate().
Code
#include <vector>
#include <iostream>
#include <numeric>
using namespace std;
int maximumWealth(vector<vector<int>>& accounts) {
int maxWealth = 0;
for (auto& account : accounts) {
maxWealth = max(maxWealth, accumulate(account.begin(), account.end(), 0));
}
return maxWealth;
}
int main() {
vector<vector<int>> accounts{{1,2,3},{3,2,1}};
cout << maximumWealth(accounts) << endl;
accounts = {{1,5},{7,3},{3,5}};
cout << maximumWealth(accounts) << endl;
accounts = {{2,8,7},{7,1,3},{1,9,5}};
cout << maximumWealth(accounts) << endl;
}
Output:
6
10
17
Complexity
- Runtime
O(m*n), wherem = accounts.length,n == accounts[i].length. - Extra space:
O(1).
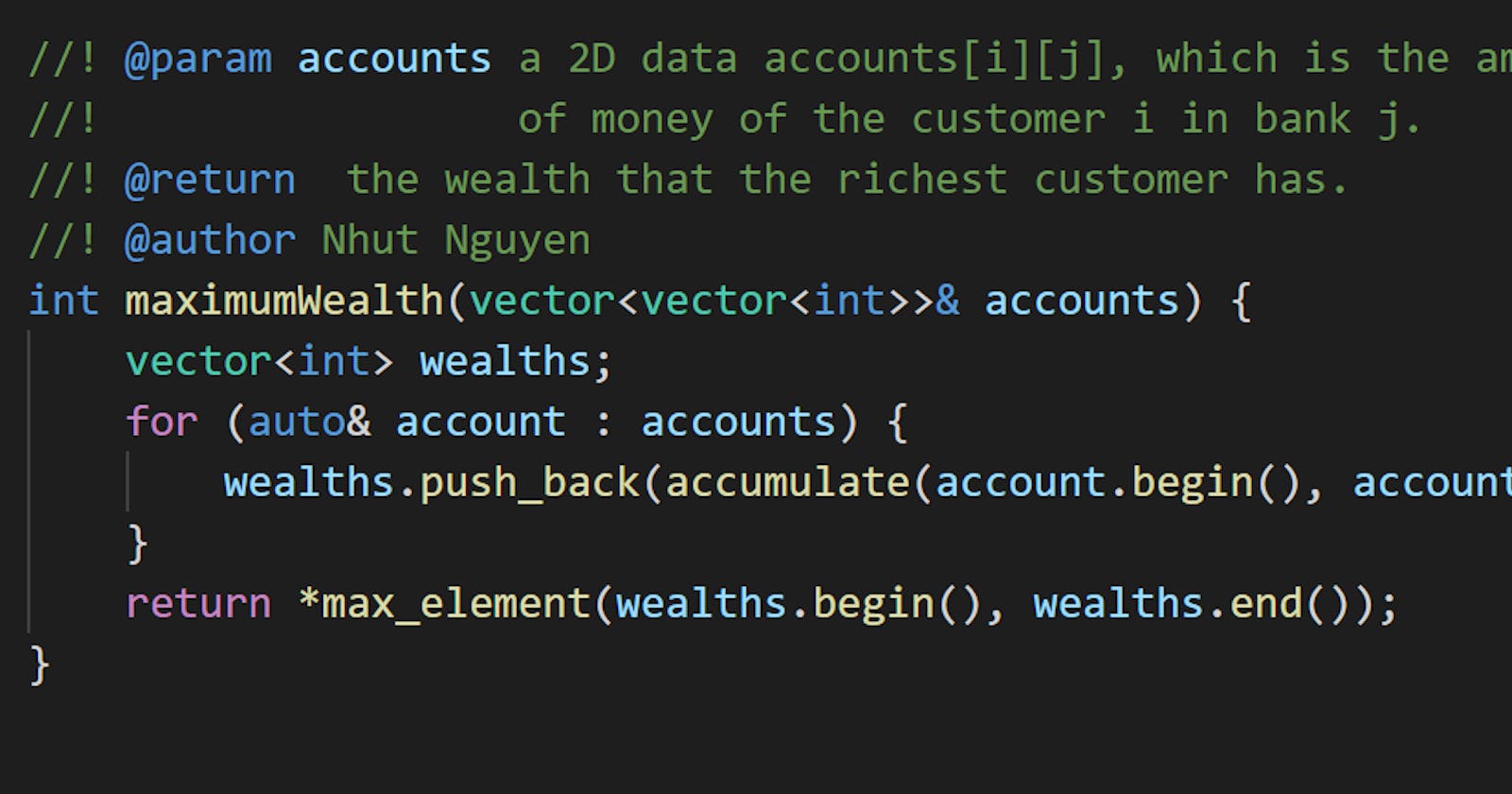
Modern C++ with std::max_element()
Depending on your application, sometimes you might want to store the wealths of all customers. Computing the maximum element of a vector is also a very common task, which can be performed by the function called std::max_element().
Code
#include <vector>
#include <iostream>
#include <numeric>
#include <algorithm>
using namespace std;
int maximumWealth(vector<vector<int>>& accounts) {
vector<int> wealths;
for (auto& account : accounts) {
wealths.push_back(accumulate(account.begin(), account.end(), 0));
}
return *max_element(wealths.begin(), wealths.end());
}
int main() {
vector<vector<int>> accounts{{1,2,3},{3,2,1}};
cout << maximumWealth(accounts) << endl;
accounts = {{1,5},{7,3},{3,5}};
cout << maximumWealth(accounts) << endl;
accounts = {{2,8,7},{7,1,3},{1,9,5}};
cout << maximumWealth(accounts) << endl;
}
Output:
6
10
17
Complexity
- Runtime
O(m*n), wherem = accounts.length,n == accounts[i].length. - Extra space:
O(1).