Problem statement

There is an integer array nums sorted in non-decreasing order (not necessarily with distinct values).

Before being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,4,4,5,6,6,7] might be rotated at pivot index 5 and become [4,5,6,6,7,0,1,2,4,4].

Given the array nums after the rotation and an integer target, return true if target is in nums, or false if it is not in nums.

You must decrease the overall operation steps as much as possible.

Example 1

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

Example 2

Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false

Constraints

• 1 <= nums.length <= 5000.
• -10^4 <= nums[i] <= 10^4
• nums is guaranteed to be rotated at some pivot.
• -10^4 <= target <= 10^4.

Solution 1: Binary search from the min element

Find the min element and do the binary search from there. When finding this min element you can check if target is found as well.

Code

#include <vector>
#include <iostream>
using namespace std;
bool search(vector<int>& nums, int target) {
    if (nums[0] == target) {
        return true;
    }
    int i = 1;
    while (i < nums.size() && nums[i - 1] <= nums[i]) {
        if (nums[i] == target) {
            return true;
        }
        i++;
    }
    int r = nums.size() - 1;
    while (i <= r) {
        int mid = i + (r - i) / 2;
        if (nums[mid] == target) {
            return true;
        } else if (nums[mid] < target) {
            i = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return false;
}
int main() {
    vector<int> nums{2,5,6,0,0,1,2};
    cout << search(nums, 0) << endl;
    cout << search(nums, 3) << endl;
    nums = {1};
    cout << search(nums, 1) << endl;
}

Output:
1
0
1

Complexity:

• Runtime: O(N), where N = nums.length.
• Extra space: O(1).

Solution 2: Generalized binary search

In order to perform the normal binary search, the array must be sorted.

So, if one of the half parts of nums is sorted, you can determine which part to go next based on the target value.

Example 2

For nums = [2,5,6,0,0,1,2] and target = 3:

• The half part [0,0,1,2] is sorted.
• The target = 3 is out of this part.
• You can go next for the part [2,5,6].
• So on and so on.

One way to identify if a part is sorted is by comparing its ends, e.g. nums[l] < nums[mid] or nums[mid] < nums[r]. In Example 2, 0 < 2 so you are sure the right half part is sorted.

The only case you are not sure which half part is sorted is when nums[l] == nums[mid] and nums[mid] == nums[r]. Especially when duplications are allowed in this problem.

In this case, you can not go for the normal binary search to any half part. The only thing you can do is shorten the nums, e.g. to [nums[l+i], ..., nums[r-j]] until you can get a new half part sorted.

Example 3

For nums = [1,0,1,1,1,1], all nums[l], nums[mid] and nums[r] are 1. There is no clear information for you to know which half part is sorted based on the comparisons between those three values. In this case, you can shorten nums to [0,1] before performing the binary search for any target.

Code

#include <vector>
#include <iostream>
using namespace std;
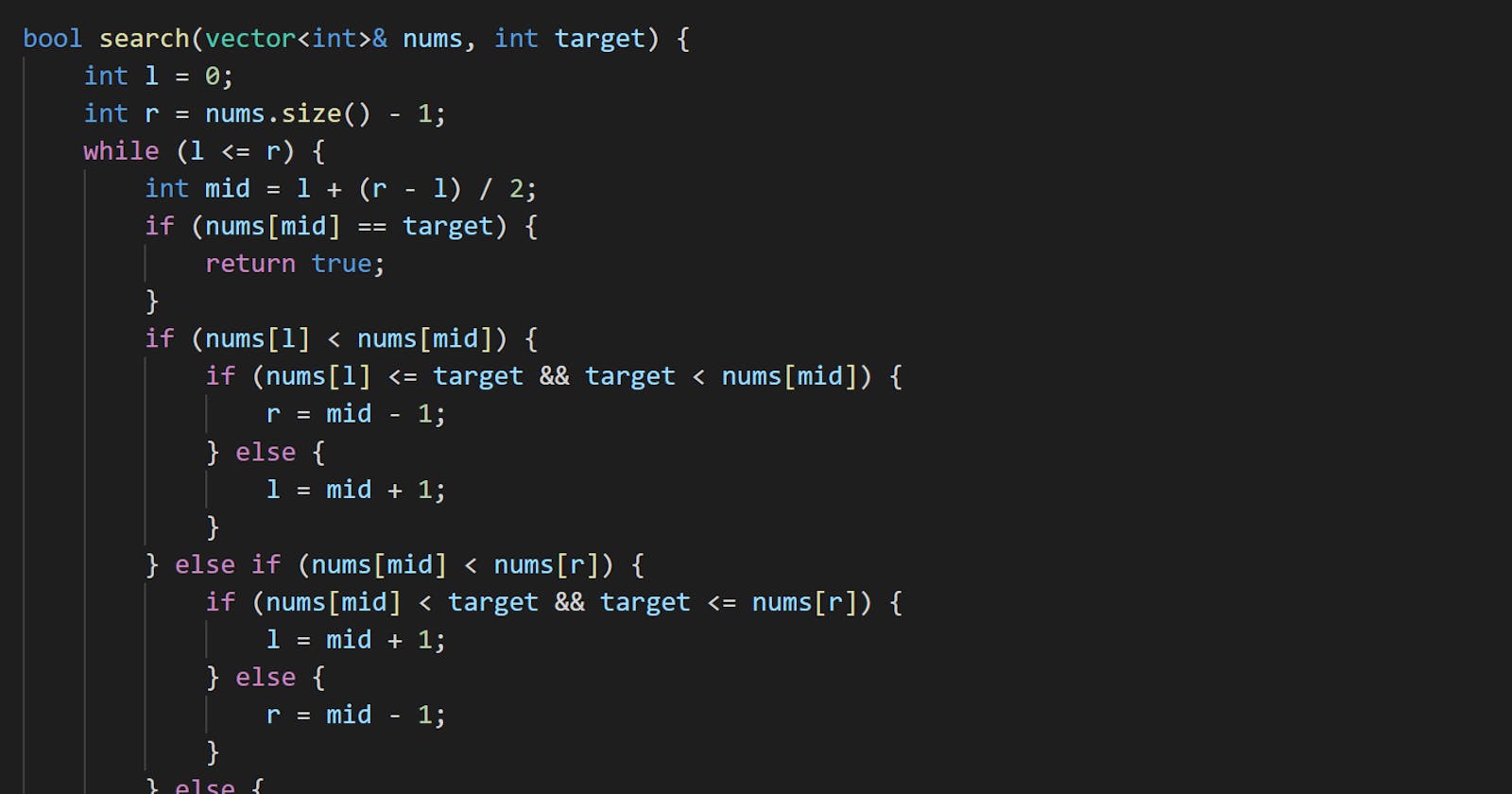
bool search(vector<int>& nums, int target) {
    int l = 0;
    int r = nums.size() - 1;
    while (l <= r) {
        int mid = l + (r - l) / 2;
        if (nums[mid] == target) {
            return true;
        }
        if (nums[l] < nums[mid]) {
            if (nums[l] <= target && target < nums[mid]) {
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        } else if (nums[mid] < nums[r]) {
            if (nums[mid] < target && target <= nums[r]) {
                l = mid + 1;
            } else {
                r = mid - 1; 
            }
        } else {
            while (l <= r && nums[l] == nums[mid]) {
                l++;
            }
            while (l <= r && nums[r] == nums[mid]) {
                r--;
            }
        }
    }
    return false;
}
int main() {
    vector<int> nums{2,5,6,0,0,1,2};
    cout << search(nums, 0) << endl;
    cout << search(nums, 3) << endl;
    nums = {1};
    cout << search(nums, 1) << endl;
    nums = {1, 0, 1, 1, 1};
    cout << search(nums, 0) << endl;
}

Output:
1
0
1
1

Complexity:

• Runtime: "Generally" O(logN), where N = nums.length. The worst case O(N) is when all elements of nums are the same value.
• Extra space: O(1).