Problem statement

An integer array is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.

For example, [1,3,5,7,9], [7,7,7,7], and [3,-1,-5,-9] are arithmetic sequences. Given an integer array nums, return the number of arithmetic subarrays of nums.

A subarray is a contiguous subsequence of the array.

Example 1

Input: nums = [1,2,3,4]
Output: 3
Explanation: We have 3 arithmetic slices in nums: [1, 2, 3], [2, 3, 4] and [1,2,3,4] itself.

Example 2

Input: nums = [1]
Output: 0

Constraints

• 1 <= nums.length <= 5000.
• -1000 <= nums[i] <= 1000.

Solution

Step 1: Find the arithmetic subarrays of nums and do not break them down

Example 1

nums = [1,2,3,4] is itself the arithmetic subarray that is not broken down into smaller ones.

Example 3

For nums = [1,2,3,4,6,8,10], [1,2,3,4] and [4,6,8,10] are the arithmetic subarrays that are not broken down into smaller ones.

Step 2: Effectively counting the smaller subarrays for each long one you found in Step 1

For each long arithmetic subarray that you found in Step 1, you need to compute how many smaller ones that have at least three elements.

For simplicity, you can assume that long arithmetic subarray is of length n and the elements are A = [a_1,a_2,...,a_n]. You might count the smaller one like following:

• Starting from a_1 you get n - 2 subarrays: [a_1, a_2, a_3], [a_1, ..., a_4], ..., [a_1, ..., a_n].
• Starting from a_2 you get n - 3 subarrays: [a_2, a_3, a_4], [a_2, ..., a_5], ..., [a_2, ..., a_n].
• And so on.
• The last one is [a_{n-2}, a_{n-1}, a_n].

In total, the number of all subarrays of A is

1 + 2 + ... + (n - 2) = (n - 2)*(n - 1)/2.

Example 1

nums = [1,2,3,4] has length n = 4.

• Starting from 1 you get n - 2 = 4 - 2 = 2 subarrays: [1,2,3] and [1,2,3,4].
• Starting from 2 you get n - 3 = 4 - 3 = 1 subarray: [2,3,4].

In total, there are 1 + 2 = 2*3/2 = 3 subarrays.

Code

#include <vector>
#include <iostream>
using namespace std;
int numberOfArithmeticSlices(vector<int>& nums) {
    if (nums.size() < 3) {
        return 0;
    }
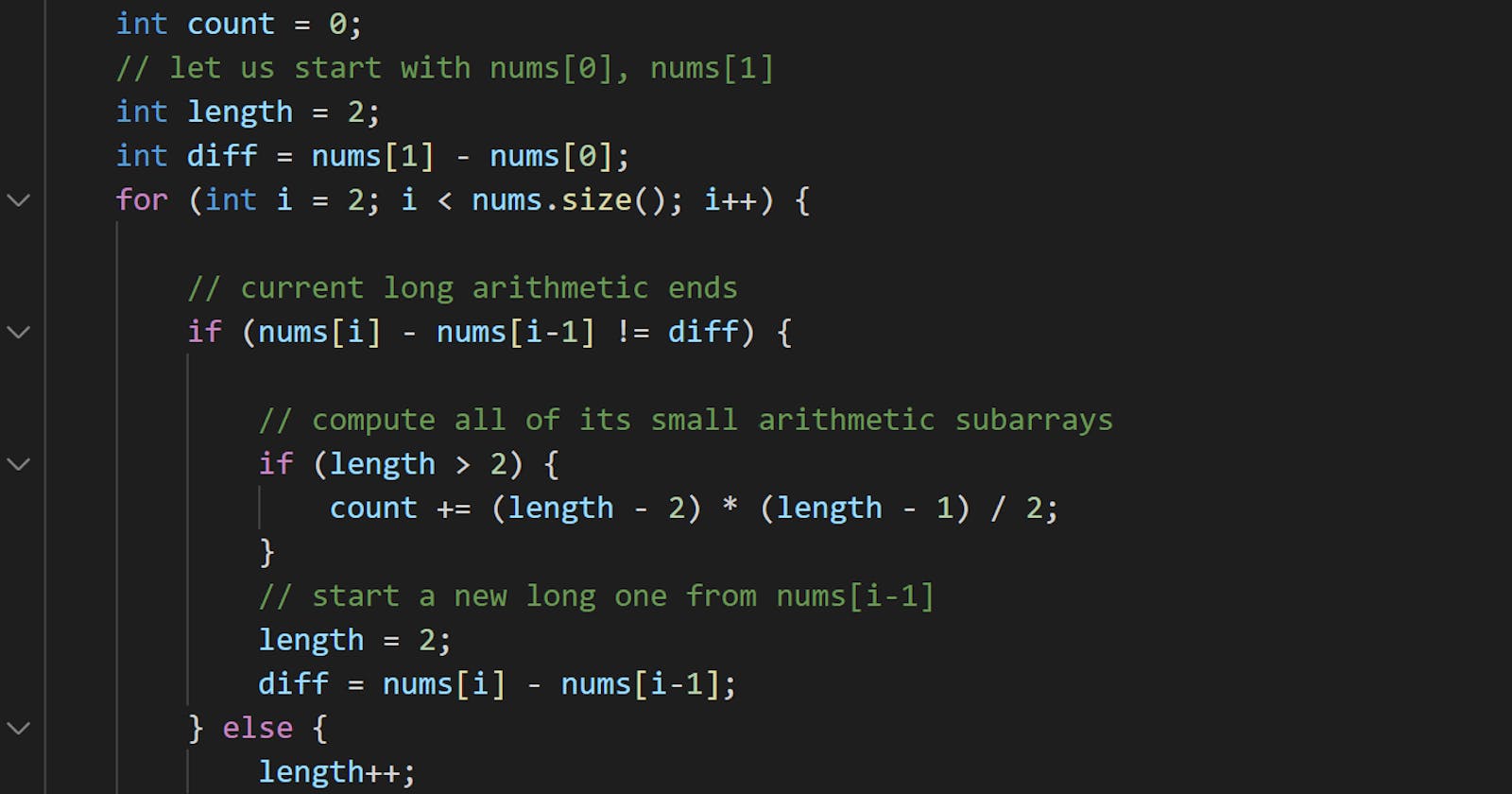
    int count = 0;
    // let us start with nums[0], nums[1]
    int length = 2;  
    int diff = nums[1] - nums[0];
    for (int i = 2; i < nums.size(); i++) {

        // current long arithmetic ends
        if (nums[i] - nums[i-1] != diff) {

            // compute all of its small arithmetic subarrays
            if (length > 2) {
                count += (length - 2) * (length - 1) / 2;
            }
            // start a new long one from nums[i-1]
            length = 2;
            diff = nums[i] - nums[i-1];
        } else {
            length++;
        }
    }
    if (length > 2) {
        count += (length - 2)*(length - 1)/2;
    }
    return count;
}
int main() {
    vector<int> nums{1,2,3,4};
    cout << numberOfArithmeticSlices(nums) << endl;
    nums = {1,2,3,4,5};
    cout << numberOfArithmeticSlices(nums) << endl;
    nums = {1};
    cout << numberOfArithmeticSlices(nums) << endl;
}

Output:
3
6
0

Complexity

• Runtime: O(N), where N = nums.length.
• Extra space: O(1).