Problem statement

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.

Example 1

Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

Example 2

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

Example 3

Input: candidates = [2], target = 1
Output: []

Constraints

• 1 <= candidates.length <= 30.
• 1 <= candidates[i] <= 200.
• All elements of candidates are distinct.
• 1 <= target <= 500.

Solution: Backtracking

If a candidate c belongs to a satisfying combination that sums to target, then you just need to solve the problem with a smaller target = target - c.

This leads to a backtracking technique to find all possible solutions for this problem.

For unique combinations, you might put the candidates in ascending order.

Example 1

For candidates = [2,3,6,7] (already sorted) and target = 7.

1. Initialize an empty solution: solution = [].
2. Starting with candidate c = 2. It might belong to some solution since it is smaller than current target = 7. Put it into current building solution, solution = [2]. Repeat the finding with target = target - c = 5.
3. c = 2 is still a valid candidate with target = 5. Put it to the current building solution solution = [2, 2]. Repeat the finding with target = 5 - 2 = 3.
4. c = 2 might still be a valid candidate with target = 3. Put it to the current building solution solution = [2, 2, 2]. Repeat the finding with target = 3 - 2 = 1.
5. There is no candidate satisfied for target = 1 at this point. The last candidate 2 of the current building solution [2, 2, 2] is not a good one. Remove it from the solution, i.e. solution = [2, 2] and target = 3. Repeat the finding with another candidate (This is called backtracking).
6. c = 3 is a perfect candidate with target = 3. This make solution = [2, 2, 3] a satisfied one for the problem.

Code

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

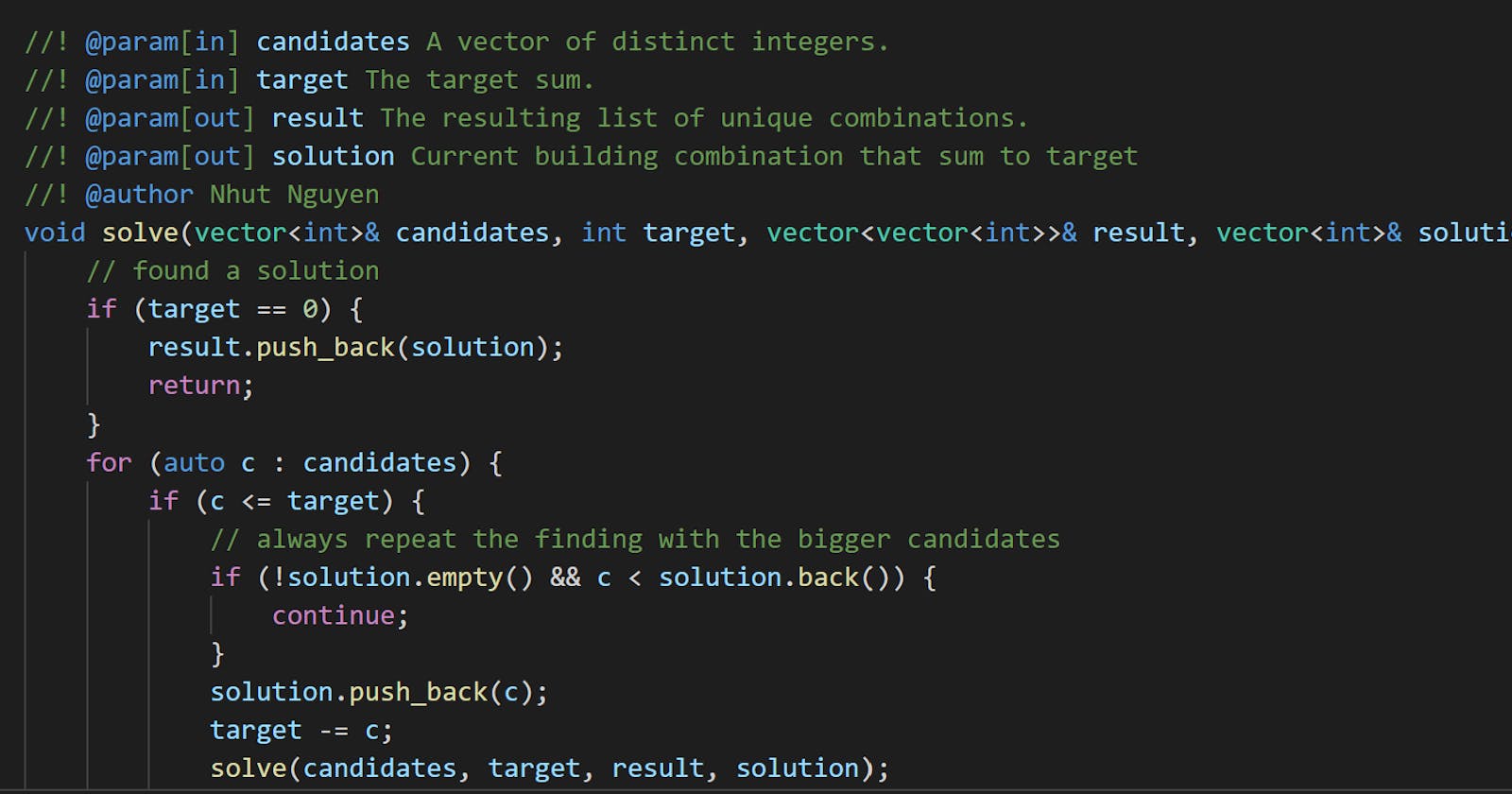
void solve(vector<int>& candidates, int target, vector<vector<int>>& result, vector<int>& solution) {
    if (target == 0) {
        result.push_back(solution);
        return;
    }
    for (auto c : candidates) {
        if (c <= target) {
            if (!solution.empty() && c < solution.back()) {
                continue;
            }
            solution.push_back(c);
            target -= c;
            solve(candidates, target, result, solution);
            if (!solution.empty()) {
                target += solution.back();
                solution.pop_back();
            }
        }
    }
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
    sort(candidates.begin(), candidates.end());
    vector<vector<int>> result;
    vector<int> solution;
    solve(candidates, target, result, solution);
    return result;
}
void print(vector<vector<int>>& result) {
    for (auto& v : result) {
        cout << "[";
        for (int a: v) {
            cout << a << ",";
        }
        cout << "]";
    }
    cout << endl;
}
int main() {
    vector<int> candidates{2,3,6,7};
    auto result = combinationSum(candidates, 7);
    print(result);
    candidates = {2,3,5};
    result = combinationSum(candidates, 8);
    print(result);
}

Output:
[2,2,3,][7,]
[2,2,2,2,][2,3,3,][3,5,]

Complexity

• Runtime: O(2^N), where N = candidates.length.
• Extra space: O(1) (if not count the space to store the result, which is O(N^2)).