Problem statement

Given an integer num, repeatedly add all its digits until the result has only one digit, and return it.

Example 1

Input: num = 38
Output: 2
Explanation: The process is
38 --> 3 + 8 --> 11
11 --> 1 + 1 --> 2 
Since 2 has only one digit, return it.

Example 2

Input: num = 0
Output: 0

Constraints

• 0 <= num <= 2^31 - 1.

Follow up: Could you do it without any loop/recursion in O(1) runtime?

Solution 1: Adding digits

Repeat the digit addition until there is only one digit remain.

Example 1

• For num = 38, its digitSum = 3 + 8 = 11 > 9 so you need to continue the process.
• Next you replace num by digitSum = 11, the new digitSum = 1 + 1 = 2 <= 9 and now you can stop.

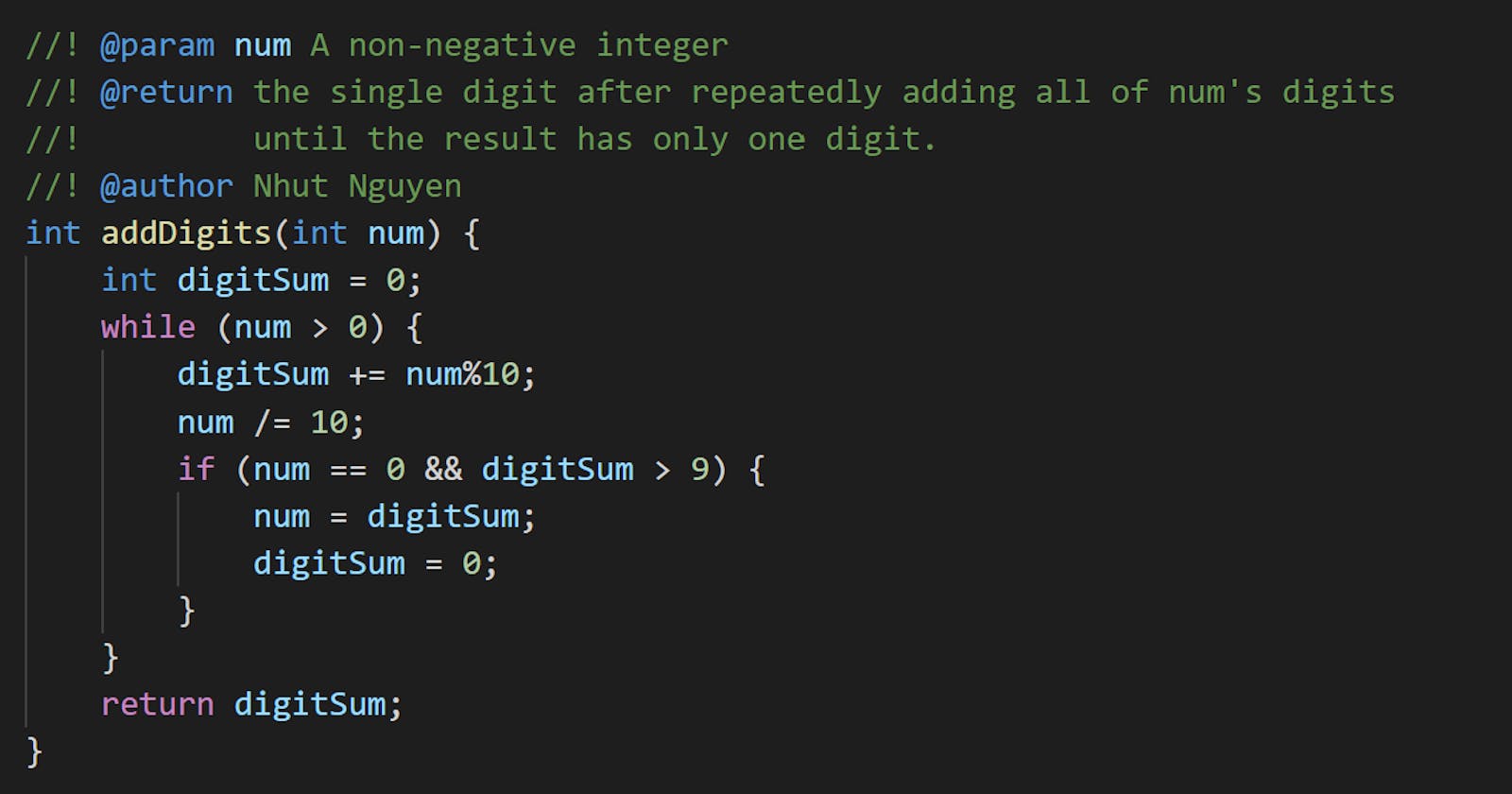
#include <iostream>
int addDigits(int num) {
    int digitSum = 0;
    while (num > 0) {
        digitSum += num % 10;
        num /= 10;
        if (num == 0 && digitSum > 9) {
            num = digitSum;
            digitSum = 0;
        }
    }
    return digitSum;
}
int main() {
    std::cout << addDigits(38) << std::endl;
    std::cout << addDigits(0) << std::endl;
    std::cout << addDigits(18) << std::endl;
}

Output:
2
0
9

Complexity

• Runtime: O(logN), where N:=num. The complexity of computing the digit sum of a number N is its number of digits, which is logN. Because digitSum is very small compared with num, the next steps converge very quickly and their complexity is very small compared with the previous ones.

• Extra space: O(1).

Solution 2: Doing the math

Example 1

If you write num = 38 = 3*9 + 3 + 8. Then the sum of its digits (3 + 8) has the same remainder as 38 when they are both divided by 9.

Example 3

If you write num = 3876 = 3*999 + 8*99 + 7*9 + 3 + 8 + 7 + 6. Then the sum of its digits (3 + 8 + 7 + 6) has the same remainder as 3876 when they are both divided by 9.

You get the finding. The final value of this problem is simply the remainder of num divided by 9.

#include <iostream>
int addDigits(int num) {
    if (num == 0) return 0;
    int result = num % 9;
    return result == 0 ? 9 : result;
}
int main() {
    std::cout << addDigits(38) << std::endl;
    std::cout << addDigits(0) << std::endl;
    std::cout << addDigits(18) << std::endl;
}

Output:
2
0
9

Complexity

• Runtime: O(1).
• Extra space: O(1).