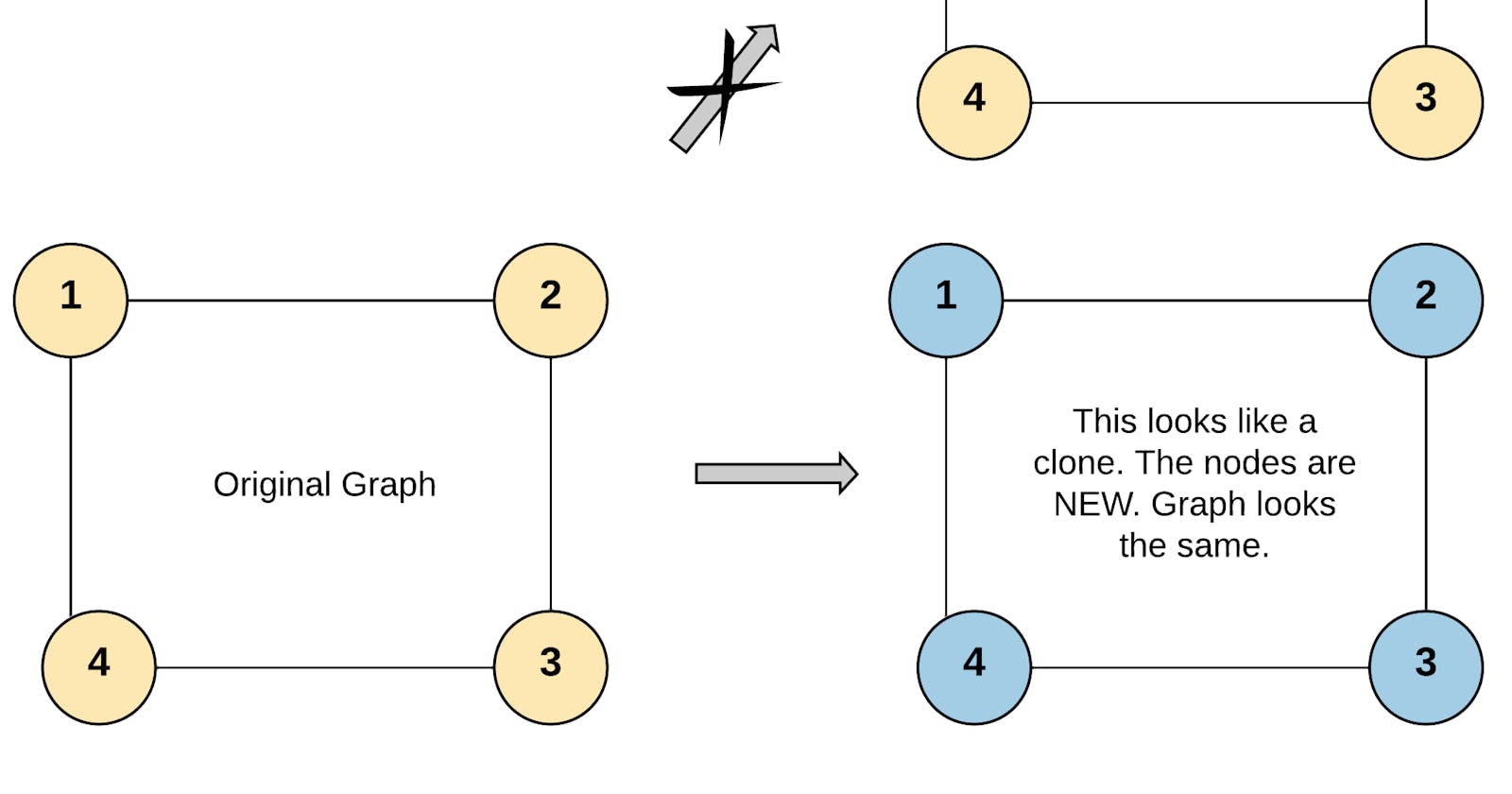
Problem statement

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format

For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.

An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1

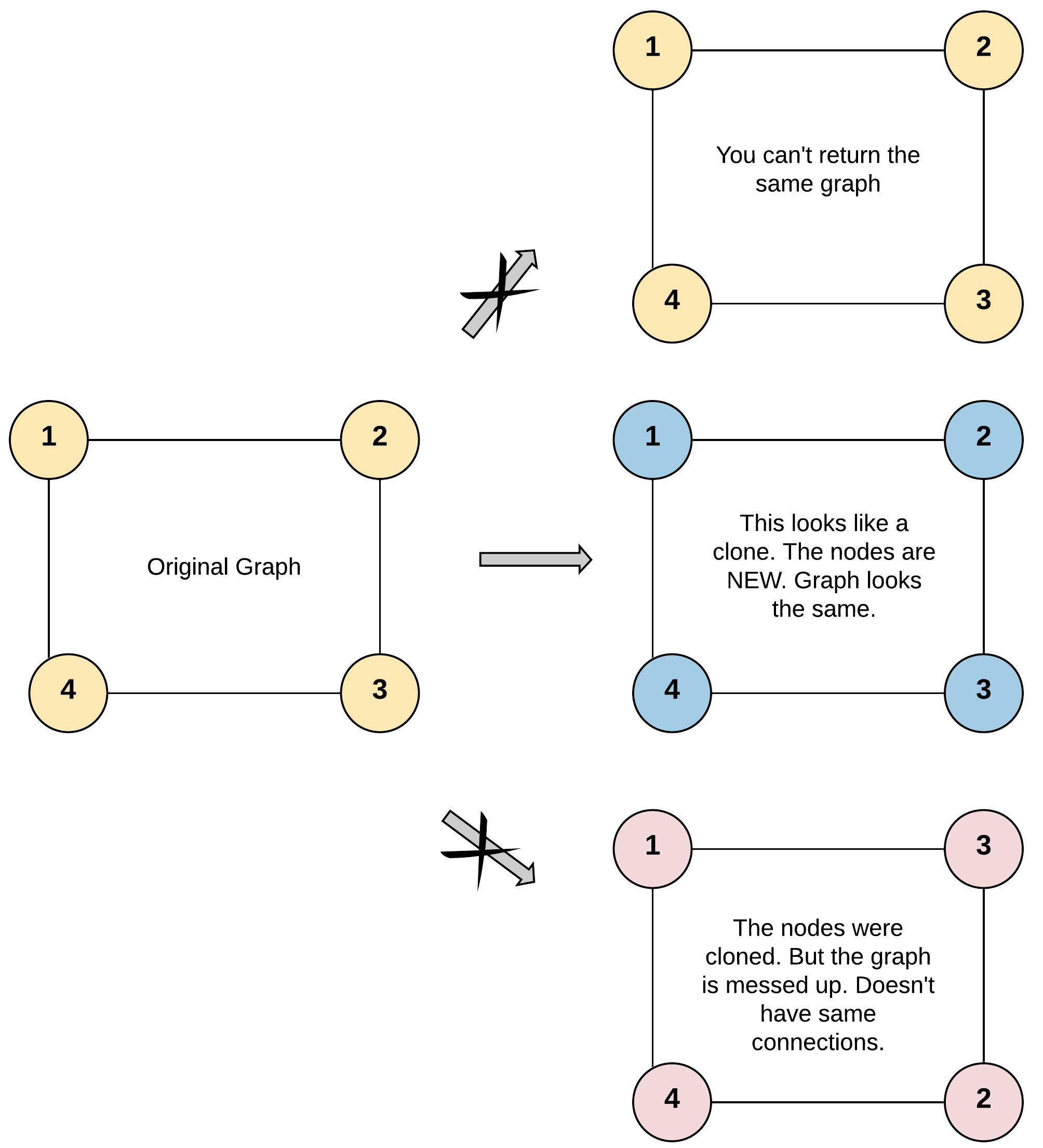
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2

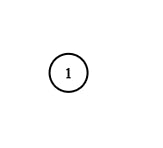
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3

Input: adjList = []
Output: []
Explanation: This is an empty graph, it does not have any nodes.

Constraints

• The number of nodes in the graph is in the range [0, 100].

• 1 <= Node.val <= 100.

• Node.val is unique for each node.

• There are no repeated edges and no self-loops in the graph.

• The Graph is connected and all nodes can be visited starting from the given node.

Solution: Cloning with marking

The most important thing when cloning a node is knowing if it was already cloned to avoid recreation.

One way of doing that is by storing the nodes that have been cloned.

Code

#include <vector>
#include <iostream>
#include <unordered_map>
using namespace std;
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};

Node* clone(Node* node, unordered_map<int, Node*>& created) {
    if (node == nullptr) {
        return nullptr;
    }
    auto it = created.find(node->val);
    if (it != created.end()) {
        return it->second;
    } 
    Node* newNode = new Node(node->val);
    created[node->val] = newNode;
    for (Node* n : node->neighbors) {
        newNode->neighbors.push_back(clone(n, created));
    }
    return newNode;
}

Node* cloneGraph(Node* node) {
    unordered_map<int, Node*> created;
    return clone(node, created);
}

void print(Node* node, unordered_map<int, int>& printed) {
    if (node == nullptr || printed[node->val] > 0) {
        return;
    }
    cout << "[";
    for (Node* n : node->neighbors) {
        cout << n->val << ",";
    }
    cout << "]";
    printed[node->val]++;;
    for (Node* n : node->neighbors) {
        print(n, printed);
    }
}

void printGraph(Node* node) {
    unordered_map<int, int> printed;
    cout << "[";
    print(node, printed);
    cout << "]\n";
}

int main() {
    {
        Node one(1);
        Node two(2);
        Node three(3);
        Node four(4);
        one.neighbors.push_back(&two);
        one.neighbors.push_back(&four);
        two.neighbors.push_back(&one);
        two.neighbors.push_back(&three);
        three.neighbors.push_back(&two);
        three.neighbors.push_back(&four);
        four.neighbors.push_back(&one);
        four.neighbors.push_back(&three);        
        printGraph(cloneGraph(&one));
    }
    {
        Node anotherOne(1);
        printGraph(cloneGraph(&anotherOne));
    }
    {
        printGraph(cloneGraph(nullptr));
    }
}

Output:
[[2,4,][1,3,][2,4,][1,3,]]
[[]]
[]

Complexity

• Runtime: O(2*M), where M is the number of graph edges. Each edge represents the neighborhood between two nodes, which is called twice, a neighbors b and b neighbors a.

• Extra space: O(N), where N is the number of graph vertices of the graph. It is for the map that stores the created nodes during the cloning.