C++ Solution to Coding Challenge 462. Minimum Moves to Equal Array Elements II
Median - The math behind the problem
Problem statement
Given an integer array nums of size n, return the minimum number of moves required to make all array elements equal.
In one move, you can increment or decrement an element of the array by 1.
Example 1
Input: nums = [1,2,3]
Output: 2
Explanation:
Only two moves are needed (remember each move increments or decrements one element):
[1,2,3] => [2,2,3] => [2,2,2]
Example 2
Input: nums = [1,10,2,9]
Output: 16
Constraints
n == nums.length.1 <= nums.length <= 10^5.-10^9 <= nums[i] <= 10^9.
Solution 1: Median - The math behind the problem
You are asked to move all elements of an array to the same value M. The problem can be reduced to identifying what M is.
First, moving elements of an unsorted array and moving a sorted one are the same. So you can assume nums is sorted in some order. Let us say it is sorted in ascending order.
Second, M must be in between the minimum element and the maximum one. Apparently!
We will prove that M will be the median of nums, which is nums[n/2] of the sorted nums.
In other words, we will prove that if you choose M a value different from nums[n/2] then the number of moves will be increased.
In fact, if you choose M = nums[n/2] + x, where x > 0, then:
Each element
nums[i]that is less thanMneeds morexmoves, while eachnums[j]that is greater thanMcan reducexmoves.But the number of
nums[i]is bigger than the number ofnums[j].So the total number of moves is bigger.
The same arguments apply for x < 0.
Example 3
For nums = [0,1,2,2,10]. Its median is 2. The minimum number of moves is 2 + 1 + 0 + 0 + 8 = 11.
If you choose M = 3 (the average value, the mean), the total number of moves is 3 + 2 + 1 + 1 + 7 = 14.
Code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int minMoves2(vector<int>& nums) {
sort(nums.begin(), nums.end());
const int median = nums[nums.size() / 2];
int moves = 0;
for (int& a: nums) {
moves += abs(a - median);
}
return moves;
}
int main() {
vector<int> nums{1,2,3};
cout << minMoves2(nums) << endl;
nums = {1,10,2,9};
cout << minMoves2(nums) << endl;
}
Output:
2
16
Complexity
Runtime:
O(nlogn), wheren = nums.length.Extra space:
O(1).
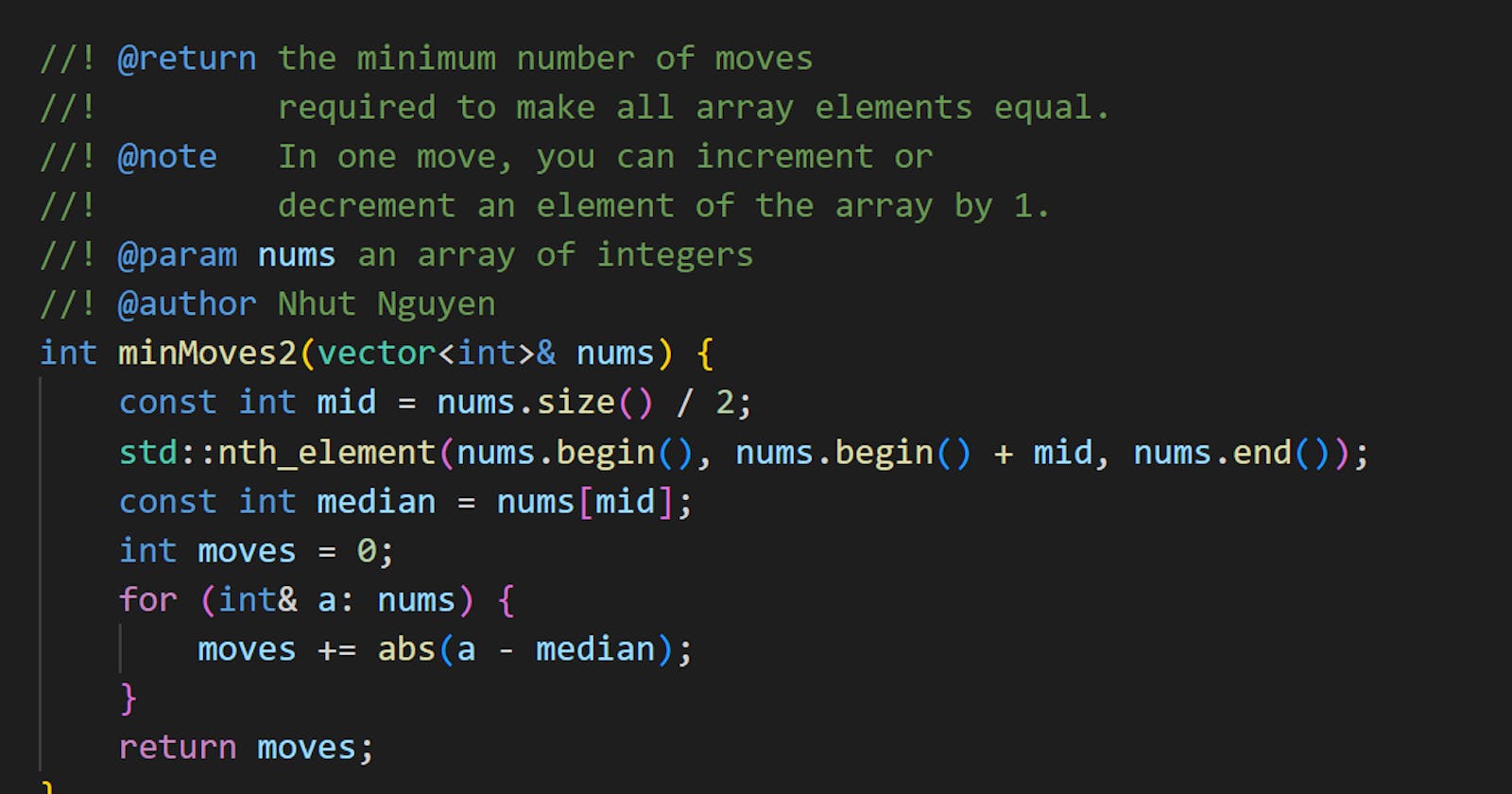
Solution 2: Using std::nth_element to compute the median
What you only need in Solution 1 is the median value. Computing the total number of moves in the for loop does not require the array nums to be fully sorted.
In this case, you can use std::nth_element to reduce the runtime complexity.
Code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int minMoves2(vector<int>& nums) {
const int mid = nums.size() / 2;
std::nth_element(nums.begin(), nums.begin() + mid, nums.end());
const int median = nums[mid];
int moves = 0;
for (int& a: nums) {
moves += abs(a - median);
}
return moves;
}
int main() {
vector<int> nums{1,2,3};
cout << minMoves2(nums) << endl;
nums = {1,10,2,9};
cout << minMoves2(nums) << endl;
}
Output:
2
16
Complexity
Runtime:
O(n), wheren = nums.length.Extra space:
O(1).
Modern C++ notes
In the code of Solution 2, the partial sorting algorithm std::nth_element will make sure for all indices i and j that satisfy 0 <= i <= mid <= j < nums.length,
nums[i] <= nums[mid] <= nums[j].
With this property, if mid = nums.length / 2 then the value of nums[mid] is unchanged no matter how nums is sorted or not.