Problem statement

Given a balanced parentheses string s, return the score of the string.

The score of a balanced parentheses string is based on the following rule:

• "()" has score 1.
• AB has score A + B, where A and B are balanced parentheses strings.
• (A) has score 2 * A, where A is a balanced parentheses string.

Example 1

Input: s = "()"
Output: 1

Example 2

Input: s = "(())"
Output: 2

Example 3

Input: s = "()()"
Output: 2

Constraints:

• 2 <= s.length <= 50.
• s consists of only '(' and ')'.
• s is a balanced parentheses string.

Recursive solution

Because s is a balanced parentheses string, it can be split into sub balanced parentheses ones. So you can follow the scoring rule to perform the recursive algorithm.

Code

#include <string>
#include <iostream>
using namespace std;
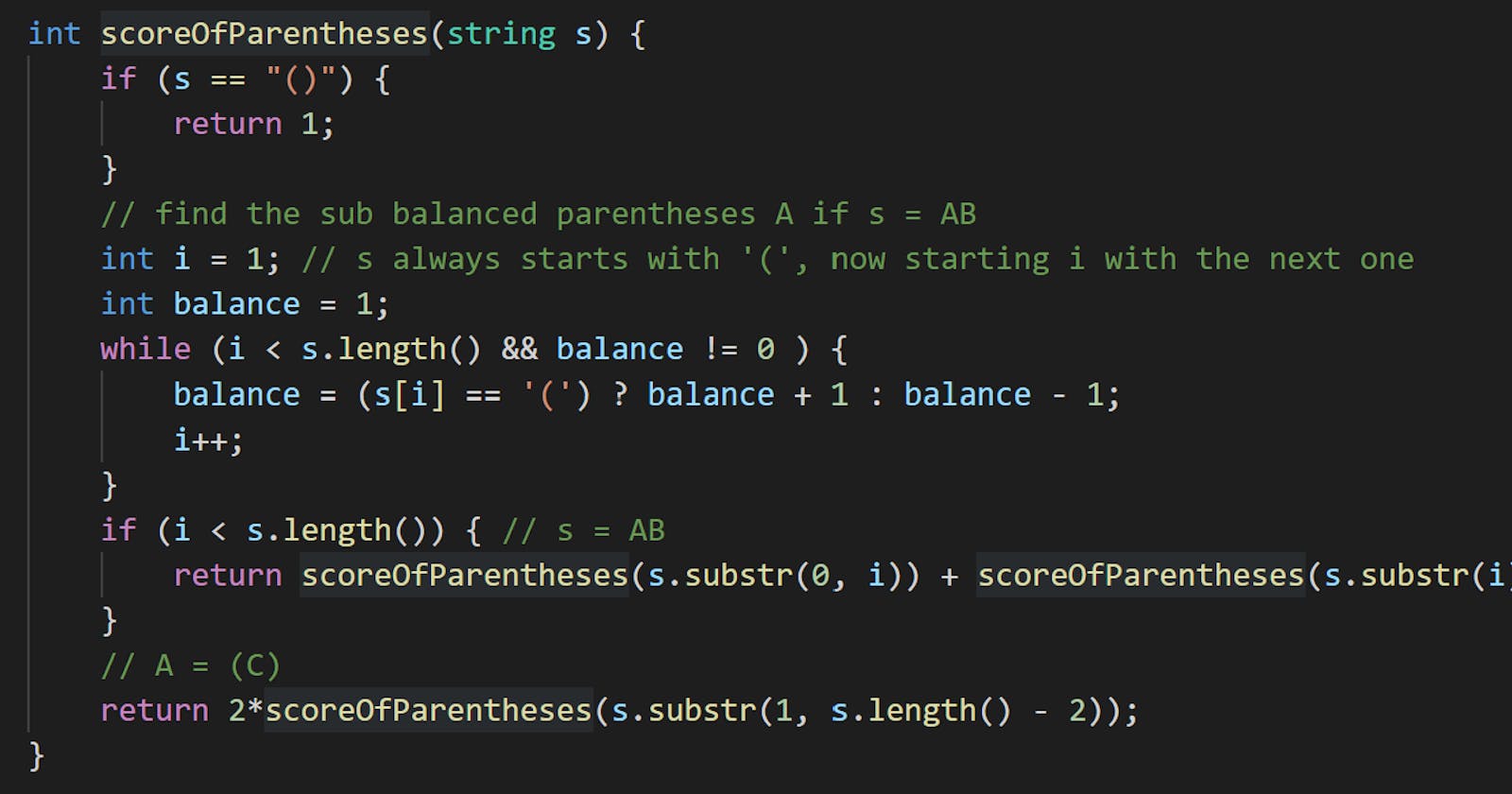
int scoreOfParentheses(string s) {
    if (s == "()") {
        return 1;
    }
    // find the sub balanced parentheses A if s = AB   
    int i = 1; // s always starts with '(', now starting i with the next one
    int balance = 1; 
    while (i < s.length() && balance != 0 ) {
        balance = (s[i] == '(') ? balance + 1 : balance - 1;
        i++;
    }
    if (i < s.length()) { // s = AB
        return scoreOfParentheses(s.substr(0, i)) + scoreOfParentheses(s.substr(i));
    }
    // A = (C) 
    return 2*scoreOfParentheses(s.substr(1, s.length() - 2));
}
int main() {
    cout << scoreOfParentheses("()") << endl;
    cout << scoreOfParentheses("(())") << endl;
    cout << scoreOfParentheses("()()") << endl;
    cout << scoreOfParentheses("(()(()))") << endl;
}

Output:
1
2
2
6

Complexity

• Runtime: O(N), where N = s.length.
• Extra space: O(logN) due to the recursive.