Problem statement
A company is planning to interview 2n people. Given the array costs where costs[i] = [aCost_i, bCost_i], the cost of flying the i-th person to city a is aCost_i, and the cost of flying the i-th person to city b is bCost_i.
Return the minimum cost to fly every person to a city such that exactly n people arrive in each city.
Example 1
Input: costs = [[10,20],[30,200],[400,50],[30,20]].
Output: 110.
Explanation:
The first person goes to city A for a cost of 10.
The second person goes to city A for a cost of 30.
The third person goes to city B for a cost of 50.
The fourth person goes to city B for a cost of 20.
The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.
Example 2
Input: costs = [[259,770],[448,54],[926,667],[184,139],[840,118],[577,469]]
Output: 1859.
Explanation: 1859 = 259 + 54 + 667 + 184 + 118 + 577.
Example 3
Input: costs = [[515,563],[451,713],[537,709],[343,819],[855,779],[457,60],[650,359],[631,42]]
Output: 3086.
Explanation: 3086 = 515 + 451 + 537 + 343 + 779 + 60 + 359 + 42.
Constraints
2 * n == costs.length.2 <= costs.length <= 100.costs.lengthis even.1 <= aCost_i, bCost_i <= 1000.
Solution: Switching flight with least sacrifice
Every candidate should fly to the city with a lower cost. But the problem requires they must share their appearance equally between the two cities. It means somebody might have to fly with a higher cost.
Because the company considers only the total cost sum, you should choose the ones that sacrifice minimal cost for their flight to make them happy to switch.
Example 2
For costs = [[259,770],[448,54],[926,667],[184,139],[840,118],[577,469]]:
- If everyone can fly with a lower cost, only the first person flies to city
a, the others fly to cityb. - But with the problem's constraint, some have to fly to city
a. The ones that have the least sacrifices in cost are the fourth one (184 - 139 = 45) and the last one (577 - 469 = 108). You can say the company only has to pay45 + 108 = 153(dollars) more for its optimal scheduling. - The final cost is
259 + 54 + 667 + 184 + 118 + 577 = 1859.
How to implement the idea
You can generalize the idea of sacrifice for all candidates.
For instance in Example 2, you might say the first one "sacrifices" 259 - 770 = -511 (dollars) as well because you will choose the ones with the least sacrifices anyway.
Code
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
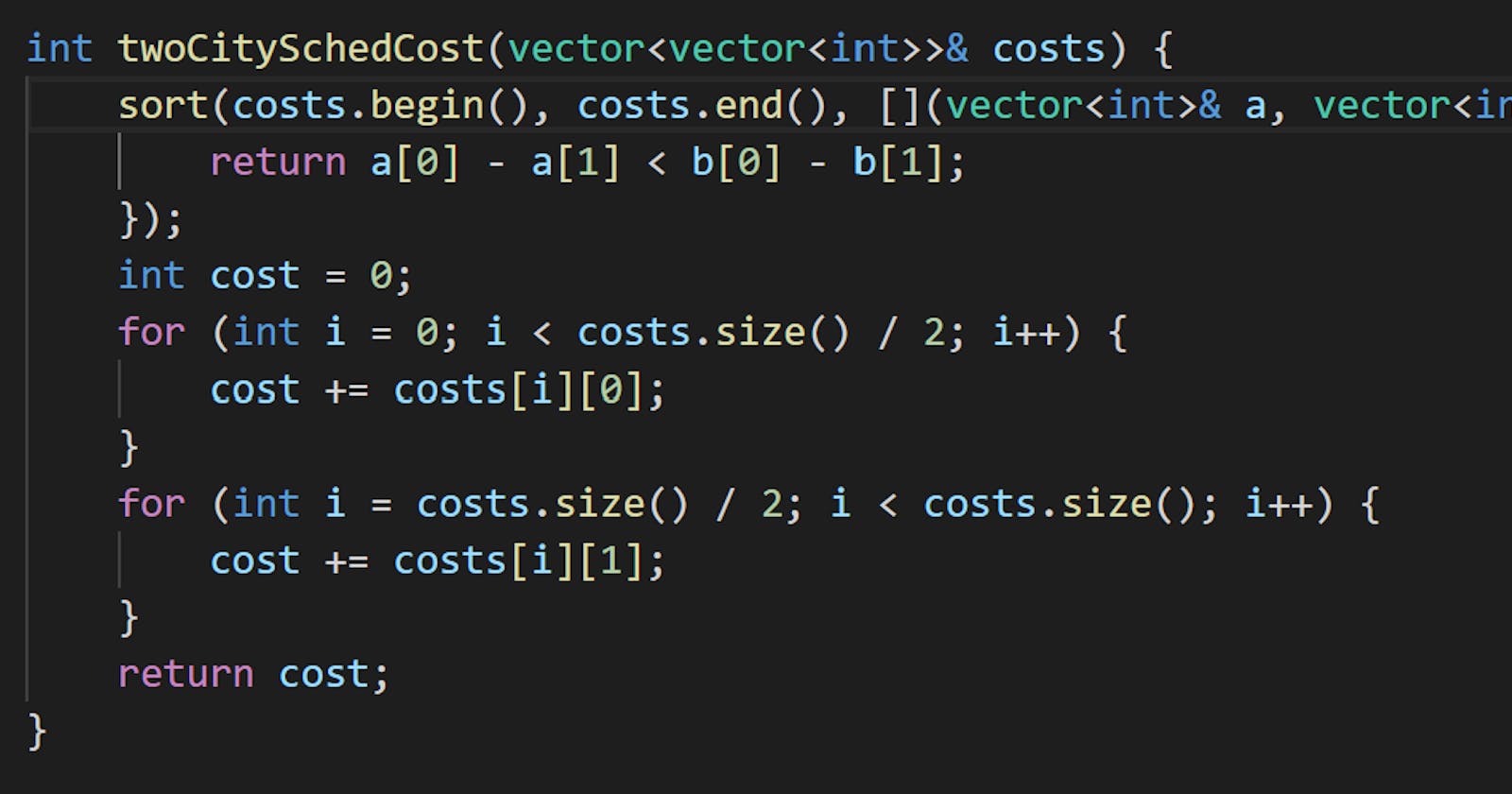
int twoCitySchedCost(vector<vector<int>>& costs) {
// sort on the sacrifices in cost
sort(costs.begin(), costs.end(), [](const vector<int>& a, const vector<int>& b){
return a[0] - a[1] < b[0] - b[1];
});
int cost = 0;
for (int i = 0; i < costs.size() / 2; i++) { // first n person
cost += costs[i][0];
}
for (int i = costs.size() / 2; i < costs.size(); i++) {
cost += costs[i][1];
}
return cost;
}
int main() {
vector<vector<int>> costs{{10,20},{30,200},{400,50},{30,20}};
cout << twoCitySchedCost(costs) << endl;
costs = {{259,770},{448,54},{926,667},{184,139},{840,118},{577,469}};
cout << twoCitySchedCost(costs) << endl;
}
Output:
110
1859
Complexity
- Runtime:
O(NlogN), whereN = costs.length. - Extra space:
O(1).