Problem statement
In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the i-th domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the i-th domino, so that tops[i] and bottoms[i] swap values.
Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.
If it cannot be done, return -1.
Example 1
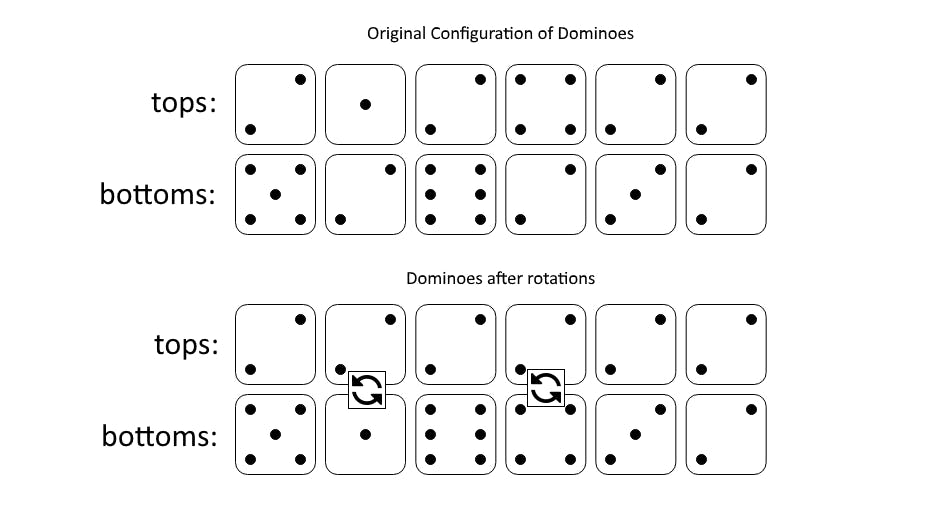
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation:
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
Example 2
Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation:
In this case, it is not possible to rotate the dominoes to make one row of values equal.
Constraints
2 <= tops.length <= 2 * 10^4.bottoms.length == tops.length.1 <= tops[i], bottoms[i] <= 6.
Solution: Count and Compare
"All the values in tops are the same" means they are equal to tops[0].
Similarly, "all the values in botoms are the same" means they are equal to bottoms[0].
You just need to compute the result for tops[0] and for bottoms[0] and compare them for the final result.
Code
#include <vector>
#include <iostream>
using namespace std;
int minDominoRotations(vector<int>& tops, vector<int>& bottoms) {
int topCount = 1;
int bottomCount = 0;
for (int i = 1; i < tops.size(); i++) {
if (tops[i] != tops[0] && bottoms[i] != tops[0]) {
tops[0] = 0;
break;
}
topCount += tops[i] == tops[0];
bottomCount += bottoms[i] == tops[0];
}
int topResult = tops[0] ? tops.size() - max(topCount, bottomCount) : -1;
if (topResult == 0) {
return 0;
}
bottomCount = 1;
topCount = 0;
for (int i = 1; i < bottoms.size(); i++) {
if (tops[i] != bottoms[0] && bottoms[i] != bottoms[0]) {
bottoms[0] = 0;
break;
}
topCount += tops[i] == bottoms[0];
bottomCount += bottoms[i] == bottoms[0];
}
int bottomResult = bottoms[0] ? bottoms.size() - max(topCount, bottomCount) : -1;
return (topResult >= 0 && bottomResult >= 0) ?
min(topResult, bottomResult) : max(topResult, bottomResult);
}
int main() {
vector<int> tops{2,1,2,4,2,2};
vector<int> bottoms{5,2,6,2,3,2};
cout << minDominoRotations(tops, bottoms) << endl;
tops = {1,2,1,1,1,2,2,2};
bottoms = {2,1,2,2,2,2,2,2};
cout << minDominoRotations(tops, bottoms) << endl;
}
Output:
2
1
Complexity
- Runtime:
O(N), whereN = tops.length. - Extra space:
O(1).
Implementation notes
- To save one or two boolean variables for flagging whether the swapping happens, you can use/modify the value of the fixed values that you choose to compare with the others. Here they are
tops[0]andbottoms[0]. - The value of a boolean expression, e.g.
tops[i] == tops[0]is casted to0(false) or1(true) when it is used in anintexpression. So you can writetopCount += tops[i] == tops[0].